
Based on my knowledge of regression analysis, I instantly knew something was fishy with both respective regressions.
The first telling sign of a weirdly interpreted model were the interactions terms, like (SO/PA)*(BB/PA).
The reason for my skepticism was mainly the interpretation of those variables.
For example, if the simple linear regression was simply the effect of SO/PA on ERA, the coefficient would be interpreted as, “for every unit change in SO/PA, ERA changes by this many units.”
However, with Fangraphs/Baseball Prospectus using interactions for rate statistics, the interpretation proves to be cloudy.
How can one explain (SO/PA)*(netGB/PA), when both variables are independent events.
There were even more fishy uses of independent variables with the modeling above, but I will choose not to retreat into the black hole of my concerns with their regression modeling.
By using Baseball Prospectus/Fangraphs’ models for SIERA as a template, I thought it would be a perfect opportunity to try to create my own metric for pitching ability, independent of fielding.
Stripping out effects of defense
As noted, in other analyses of true pitcher ability, earned runs and ERA can be affected by the pitcher’s defense around him.
In order to properly gauge true pitcher ability, we must strip out a team’s defensive ability out of earned runs. Thus, we use the equation:
(2) Earned Runs Average = β0 + β1 * (UZR) + µ
From this regression, we can use the residuals (µ) as a dependent variable in a future equation.
A New Adjusted SIERA model
(3)

(4)

Next, we can run a regression of the residuals (µ) from the previous equation on many different variations of independent variables.
After testing the regression model, the most significant variables towards explaining Earned Runs Prevented Average (ERPA) proved to be Strikeouts per Plate Appearance (SO/PA), Walks per Plate Appearance (BB/PA), and Net Result of Groundballs minus Flyballs per Plate Appearance (netGB/PA).
Now, it is important to interpret the coefficients for all of the variables for the model.
In the data set, the standard deviation for SO/PA for all MLB teams from 2010 to 2014 was about 4.61%.
Thus, for every 4.61% increase in SO/PA, ERPA will decrease by .5728 runs on average. For every standard deviation increase in BB/PA, ERPA will increase by .2584 runs on average.
While, every standard deviation increase in netGB/PA will decrease ERPA by .2708 runs on average.
Most people will judge an R^2 of 50.45% as low because it does not reach some threshold R^2 of 85%.
In terms of the predictive power of a pitcher’s ability, a 50.45% R^2 can be considered justifiable.
As shown in (4), the P-Value for the model is significant towards ERPA. To clarify our R^2, 50.45% of the variation in ERPA is explained by our independent variables SO/PA, BB/PA, and netGB/PA.
Conclusion
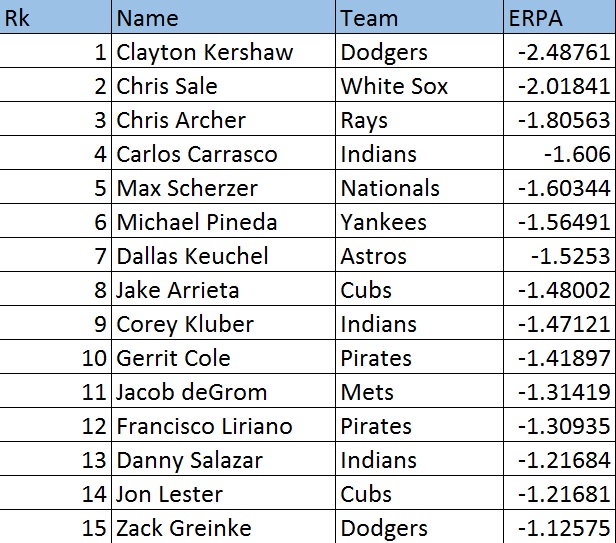
Finally, we can plug in our values for SO/PA, BB/PA, and GBnet/PA into our equation and produce values for all pitchers in Major League baseball.
Now, we can revisit our top fifteen chart from before.
Based on our predictive measure, Clayton Kershaw has proven to be the most dominant pitcher in the game.
Although other pitchers like Zack Greinke and Gerrit Cole have gained more praise for their performance this season, Kershaw has all of the peripherals (SO/PA of 33.6%, BB/PA of 4.9%, and a high GBnet/PA) of the “ideal” pitcher every team wants.
A large drawback of this predictive formula for ERPA is the lack of accountability for hit quality.
Although a pitcher has control of being either a groundball or flyball pitcher, the predictive model for ERPA is essentially penalizing flyball pitchers because of the sole reason that the expected runs from a flyball is higher than a groundball.
In future formulations, the use of play-by-play data would be more effective for measuring a pitcher’s ability and would allow for flyball pitchers to be properly evaluated. By using play-by-play data, one could possibly use more detailed variables like Strikes Swinging, Batted Ball distance, Batted Ball Speed, and many more variables.
Consequently, this would result in a more precise metric for ERPA.
However, with accurately detailed play-by-play events not available at my disposal, the model for ERPA improves upon the predecessor of Baseball Prospectus’ and Fangraphs’ SIERA measurement.
With this measurement, we can now properly measure a pitcher’s ability on variables that a pitcher can control.
References:
1. Swartz, Matt. "New SIERA, Part Two (of Five): Unlocking Underrated Pitching Skills | FanGraphs Baseball." New SIERA, Part Two (of Five): Unlocking Underrated Pitching Skills | FanGraphs Baseball. Fangraphs, 11 July 2011. Web. 29 July 2015.
2. "Baseball Statistics and Analysis | FanGraphs Baseball." Baseball Statistics and Analysis | FanGraphs Baseball. N.p., n.d. Web. 24 Apr. 2015.
NOTE: All statistics accurate as of 08/03/15
By Sanjay Pothula
AriBall.com




